반응형
회귀 분석(Regression) 알고리즘 구현하기
이번 실습에서는 간단한 파이썬 코드 작성을 통해 회귀 분석 알고리즘을 구현해보도록 하겠습니다.
이론 강의를 통해 회귀 모델은 다음과 같이 표현한다고 하였습니다.
Y=β0+β1X
여기서 적절한 β0 와 β1 를 찾기 위해서는 데이터의 실제 값과 모델이 예측하는 값의 차이를 최소한으로 하는 선을 찾아야 합니다.
차이를 최소한으로 하는 선을 찾는 회귀 분석의 절차는 다음과 같습니다.
회귀 분석의 절차
- X라는 값이 입력되면 Y=β0+β1X라는 계산식을 통해 값을 산출하는 예측 함수를 정의합니다.
- 실제 값 y와 예측 함수를 통해 도출된 예측값 pred_y간의 차이를 계산합니다.
- 계산한 차이에 기반하여 β0와 β1를 업데이트하는 규칙을 정의하고 이를 바탕으로 β0와 β1의 값을 조정합니다.
- 위의 과정을 특정 반복 횟수(iteration) 만큼 반복합니다.
- 반복적으로 수정된 β0와 β1를 바탕으로 Y=β0+β1X라는 회귀식을 정의합니다.
실습
- beta_0, beta_1, X 를 받아서 예측값 y_pred를 계산하여 반환하는 prediction() 함수를 구현합니다.
- 반복 횟수만큼 오차(loss)를 계산하고 beta_0,beta_1의 값을 변경하는 함수인 gradient_descent() 를 구현합니다.
- 실행 버튼을 눌러 회귀 분석 과정의 시각화를 확인합니다.
- 제출 버튼을 눌러 올바른 회귀 알고리즘 구현 여부를 확인합니다.
Tips!
- const function으로 MSE를 사용
import numpy as np
import matplotlib.pyplot as plt
from elice_utils import EliceUtils
elice_utils = EliceUtils()
# 데이터를 생성하고 반환하는 함수입니다.
def load_data():
X = np.array([[8.70153760], [3.90825773], [1.89362433], [3.28730045], [7.39333004], [2.98984649], [2.25757240], [9.84450732], [9.94589513], [5.48321616]])
y = np.array([[5.64413093], [3.75876583], [3.87233310], [4.40990425], [6.43845020], [4.02827829], [2.26105955], [7.15768995], [6.29097441], [5.19692852]])
return X, y
"""
1. 입력값(X)과 beta_0,beta_1를 바탕으로
예측값(pre_y)을 계산하여 반환하는 함수를 구현합니다.
회귀 함수 식을 참고하여
예측값을 계산합니다.
"""
def prediction(beta_0, beta_1, X):
y_pred = beta_0 + beta_1 * X
return y_pred
# beta_1와 beta_1 값을 업데이트 하는 규칙을 정의하는 함수입니다.
def update_beta(X, y, y_pred, lr):
delta_0 = -(lr * (2 / len(X)) * np.sum(y - y_pred))
delta_1 = -(lr * (2 / len(X)) * (np.dot(X.T, (y - y_pred))))
return delta_0, delta_1
"""
2. 반복 횟수만큼 오차(loss)를 계산하고
beta_0,beta_1의 값을 변경하는 함수를 구현합니다.
Step01. 실제 값 y와 prediction 함수를 통해 예측한
예측 값 pred_y 간의 차이(loss)를 계산합니다.
loss는 실제값(y) - 예측값(pred_y)으로 정의하겠습니다.
Step02. 구현된 함수를 이용하여
beta_0와 beta_1 의 변화값을 각각 beta0_delta, beta1_delta에 저장합니다.
"""
def gradient_descent(X, y, iters, lr):
beta_0 = np.zeros((1,1))
beta_1 = np.zeros((1,1))
for i in range(iters):
y_pred = prediction(beta_0, beta_1, X)
loss = np.mean(np.square(y - y_pred))
beta0_delta, beta1_delta = update_beta(X, y, y_pred, lr)
beta_0 -= beta0_delta
beta_1 -= beta1_delta
# 100번의 학습마다 그래프 출력하기
if i%100==0:
print("학습 횟수 :",i)
plotting_graph(X,y,beta_0,beta_1)
return beta_0, beta_1
# 그래프를 시각화하는 함수입니다.
def plotting_graph(X,y,beta_0,beta_1):
y_pred = beta_0 + beta_1[0,0] * X
fig = plt.figure()
plt.scatter(X, y)
plt.plot(X, y_pred,c='r')
plt.savefig("test.png")
elice_utils.send_image("test.png")
# 회귀 알고리즘 구현 진행을 위한 main() 함수입니다.
def main():
# 학습을 위해 필요한 파라미터입니다.
lr = 1e-4
iteration = 1000
X, y = load_data()
beta_0, beta_1 = gradient_descent(X, y, iteration, lr)
print("{}번의 학습 이후의 회귀 알고리즘 결과".format(iteration))
print("beta_0:",beta_0[0], "beta_1:",beta_1[0])
plotting_graph(X,y,beta_0,beta_1)
return beta_0, beta_1
if __name__=="__main__":
main()
학습 횟수 : 0 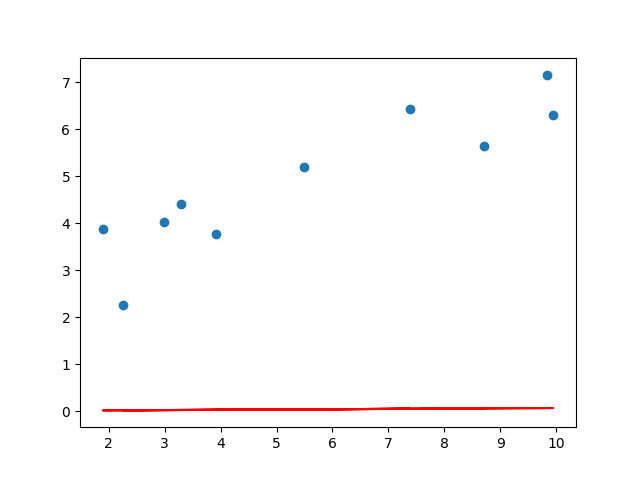
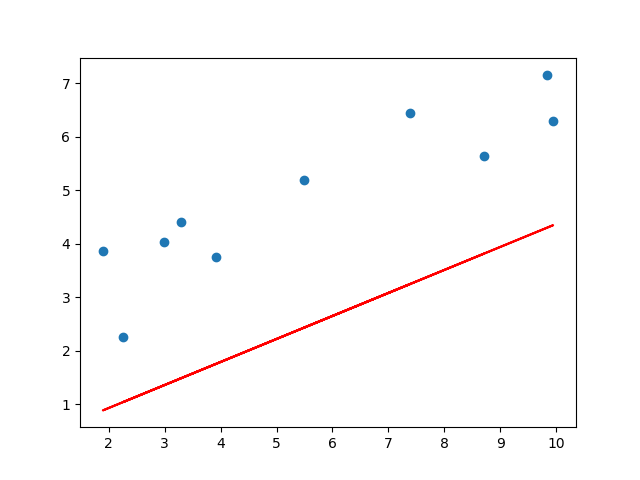
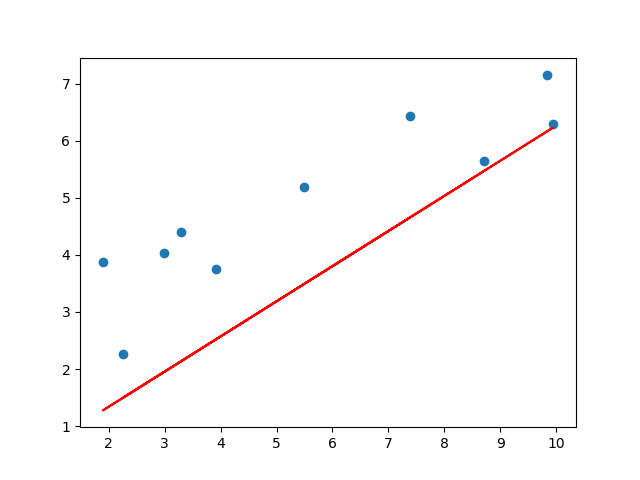
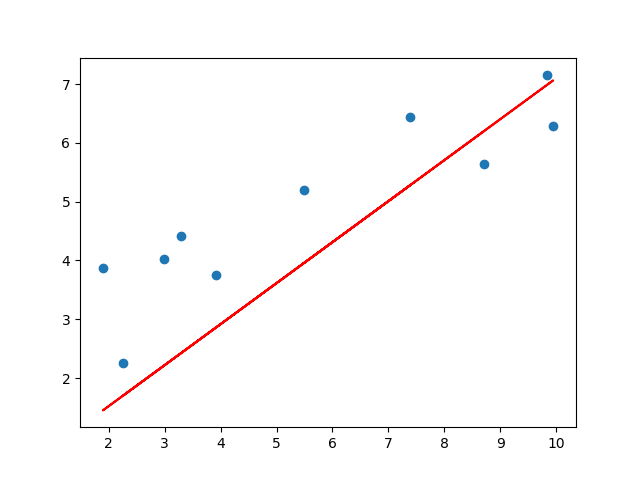
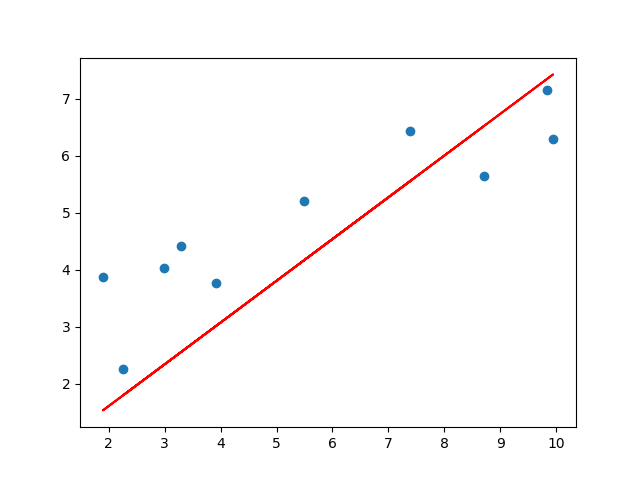
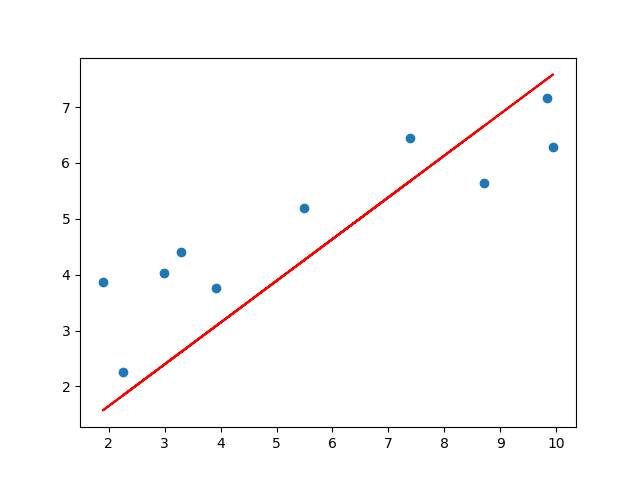
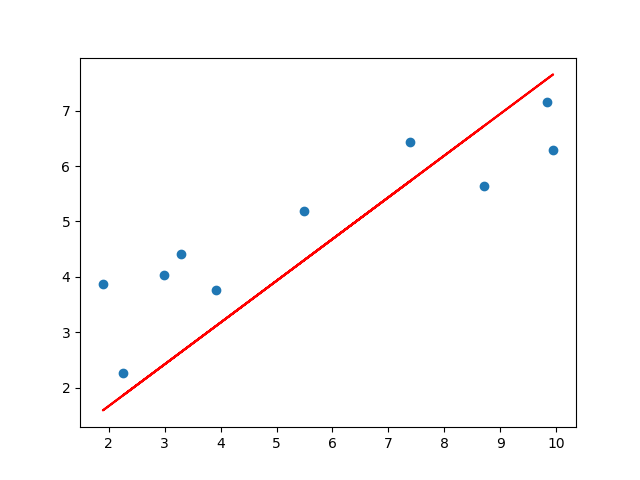
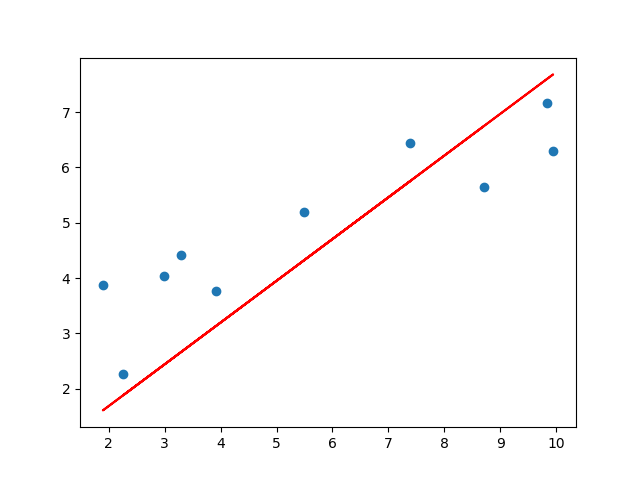
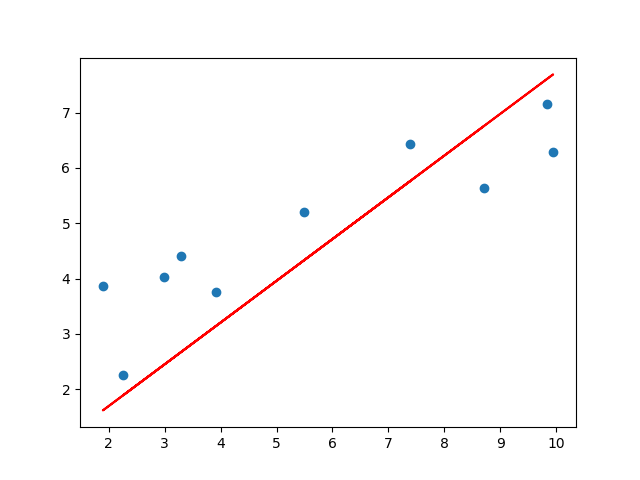
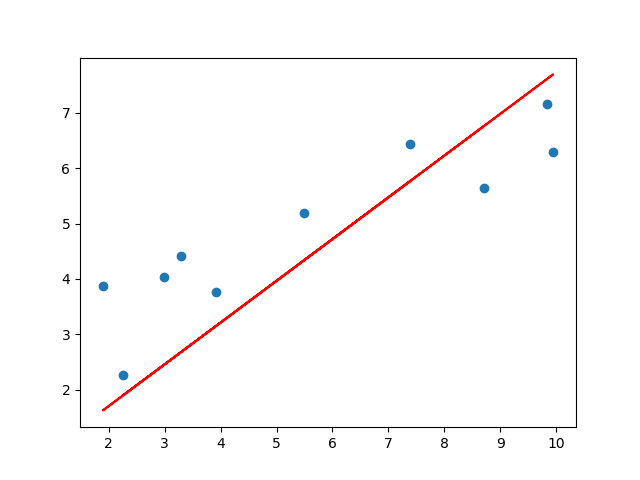










beta_0: [0.21056]
beta_1: [0.75204095] 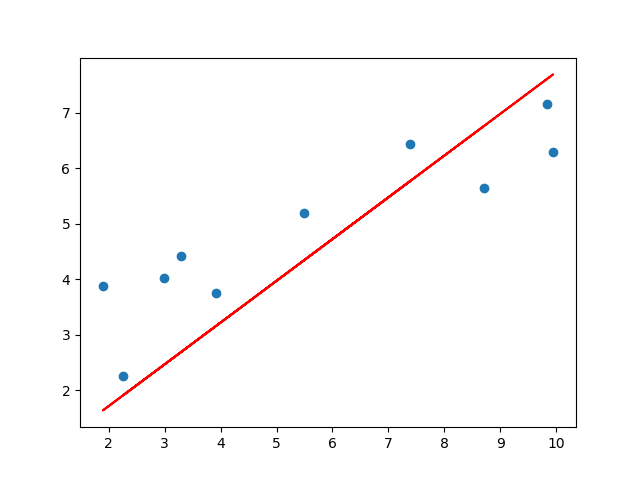


반응형
'AI & 머신러닝 coding skill' 카테고리의 다른 글
| 머신러닝 - 과적합 방지 기법 - 교차 검증 (0) | 2022.05.23 |
|---|---|
| 머신러닝 - 다항 회귀 모델 구현하기 (0) | 2022.05.23 |
| 머신러닝 - 다중 선형 회귀 모델 구현하기 (0) | 2022.05.23 |
| 머신러닝 - 회귀(Regression) 사이킷런 (0) | 2022.05.23 |
| 가상 PC 서버 window에서 OS 시간 및 언어 설정 (0) | 2022.04.03 |
| 아마존 AWS Deep racer - 7,8월 리그 결과, RC car 테스트 시작 (0) | 2021.12.21 |
| 아마존 AWS Deep racer - 6월 리그 결과, Pro division 승격! (0) | 2021.07.25 |
| 아마존 AWS DeepRacer - 강화학습 교육 이수증 (0) | 2021.06.15 |



