반응형
주성분 분석(PCA)
PCA를 사용하면 가장 덜 중요한 축들은 제거되고, 가장 중요한 상위 축만 남겨집니다.
이렇게 데이터 내에서 영향을 덜 주는 변수들이 사라지면, 점들 간에 가장 중요한 관계를 맺는 차원들만을 남길 수 있습니다.
예를 들어, 변수를 반으로 줄였을 때 대부분의 점들이 잘 보존된다면, 적은 정보로 값을 그대로 표현할 수 있어 데이터를 사용하기에 훨씬 효율적일 것입니다.
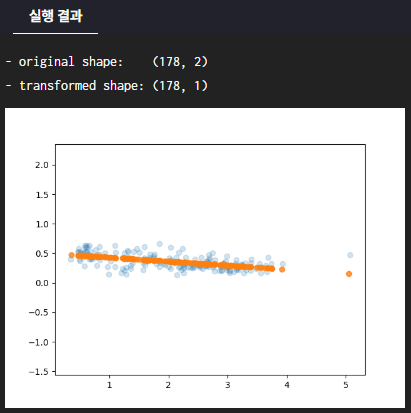
이번 실습에서는 2차원으로 고정한 wine data를 주성분이 있는 PCA를 사용하여 1차원으로 축소할 때 결과를 확인해보도록 하겠습니다.
PCA를 위한 사이킷런 함수/라이브러리
- from sklearn.decomposition import PCA : 사이킷런에 구현되어 있는 주성분 분석(PCA) 모델을 불러옵니다.
- PCA(n_components): n_components 개수로 데이터의 차원을 축소하도록 주성분 분석을 정의합니다.
- [Model].fit(data) : data에 대해 차원 축소를 위한 학습을 진행합니다.
- [Model].transform(data): data를 설정한 n_components 으로 차원을 축소시킨 결과 데이터를 반환합니다.
from elice_utils import EliceUtils
elice_utils = EliceUtils()
import numpy as np
from sklearn.decomposition import PCA
from sklearn.datasets import load_wine
import matplotlib.pyplot as plt
"""
1. 사이킷런에 저장된 데이터를 불러오고,
2개의 변수만을 가질 수 있도록
고정하여 반환하는 함수를 구현합니다.
Step01. 사이킷런에 저장된 데이터를 불러옵니다.
데이터는 (X, y) 형태로 불러와야 합니다.
Step02. column_start로 지정된 특정 column으로부터
연속되는 2개의 변수를 X에 저장합니다.
"""
def load_data():
X, y = load_wine(return_X_y = True)
column_start = 6
X = X[:, column_start : column_start + 2]
return X
"""
2. 주성분 분석(PCA)을 수행하여
2차원 데이터를 1차원으로 축소하는 함수를 완성합니다.
Step01. PCA의 n_components를 1로 지정하여
pca 를 정의합니다.
Step02. 주성분 분석을 수행합니다.
Step03. X_pca 값을 추출합니다.
"""
def pca_data(X):
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
return pca, X_pca
# 축소된 주성분 축과 데이터 산점도를 그려주는 함수입니다.
def visualize(pca, X, X_pca):
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');
plt.savefig('PCA.png')
elice_utils.send_image('PCA.png')
def main():
X = load_data()
pca, X_pca = pca_data(X)
print("- original shape: ", X.shape)
print("- transformed shape:", X_pca.shape)
visualize(pca, X, X_pca)
if __name__ == '__main__':
main()

반응형
'AI & 머신러닝 coding skill' 카테고리의 다른 글
| 머신러닝 의사결정 나무(DecisionTree Classifier) - 분류 (0) | 2022.05.24 |
|---|---|
| 머신러닝 의사결정 나무(DecisionTree Regressor) - 회귀 (0) | 2022.05.24 |
| 머신러닝 - 이진트리 분류기 만들기 (0) | 2022.05.24 |
| 머신러닝 - t-SNE (0) | 2022.05.23 |
| 머신러닝 Clustering - K-Means VS GMM (0) | 2022.05.23 |
| 머신러닝 Clustering - Gaussian Mixture Model (GMM) (0) | 2022.05.23 |
| 머신러닝 Clustering - K-Means 클러스터링 (0) | 2022.05.23 |
| 머신러닝 분류 - 로지스틱 회귀(Logistic Regression) (0) | 2022.05.23 |



